Die
23. Runde und damit die in unseren Augen schwierigste von allen jemals beim Schlaumeier gestellten Aufgaben, ist nun zu Ende. Die richtigen Ergebnisse lauteten:
a) 00:43:35 Stunden
b) 01:25:27 Stunden
Zu a)
Gegeben ist die Laufzeit eines Transportboots von Stadt A zu Stadt B. Eine solche Laufzeit setzt sich immer aus der sog. Rüstzeit und der sog. Marschzeit zusammen (
s. Wiki). Die Rüstzeit ist einzig und allein abhängig von der Weltgeschwindigkeit. Die Marschzeit hingegen hängt von der Entfernung zwischen zwei Punkten auf der Karte sowie der Geschwindigkeit der langsamsten Einheit eines Befehls ab.
Die angegebene Laufzeit von 1:41:33 Stunden ist nun laut Aufgabenstellung zunächst in Sekunden umzurechnen:
1 * 60 * 60 + 41 * 60 + 33 = 6093 Sekunden
Wir trennen nun die Rüst- und Marschzeit voneinander:
Die Rüstzeit beträgt
15 Minuten / Weltgeschwindigkeit, in diesem Fall also 15 / 1 = 15 Minuten = 900 Sekunden.
Die Rüstzeit beträgt also 900 Sekunden, die Marschzeit 6093 - 900 = 5193 Sekunden.
Da wir die Laufzeit für den Befehl bei einem Weltspeed von 3 bestimmen sollen, muss die Rüstzeit für den Befehl 15 Minuten / 3 = 5 Minuten = 300 Sekunden betragen. Die Rüstzeit ist somit klar und wir konzentrieren uns nun auf die Marschzeit, bevor wir beides aufaddieren und die Laufzeit angeben können.
Für die Marschzeit ist nun (bei ja gleichbleibender Entfernung) die Geschwindigkeit der Einheit entscheidend, um zu berechnen, wie lange sie für die Strecke braucht. Je höher die Geschwindigkeit, desto kürzer die Marschzeit. Geschwindigkeit und Marschzeit verhalten sich also antiproportional zueinander.
Zuerst einmal ist es daher wichtig, die Geschwindigkeit des Transportboots zu bestimmen, die es hat, wenn es 5193 Sekunden Marschzeit braucht.
Ein Transportboot hat
laut Wiki eine Geschwindigkeit von 8. Zu beachten ist allerdings, dass der Einheitenspeed 2 beträgt - die Geschwindigkeit beträgt dann also 16. Die Aussage ist: bei einer Geschwindigkeit von 16 beträgt die Marschzeit für das Transportboot 5193 Sekunden.
Die Frage, die wir uns nun stellen: Inwiefern verändern die geänderten Bedingungen in Teilaufgabe a) die Geschwindigkeit, für welche Geschwindigkeit des Transportboots muss ich dann also am Ende die Marschzeit bestimmen?
Folgende Faktoren spielen dabei eine Rolle:
- Transportboot: Geschwindigkeit 8
- Einheitenspeed 3
- Bonus "Verbesserte Truppenbewegung": Einheiten bewegen sich 30% schneller
- Spezialgebäude "Leuchtturm": Einheiten bewegen sich 15% schneller
- nicht: Forschung "Segel setzen", denn diese macht nur Kolonieschiffe um 10% schneller
Ein Knackpunkt (vor allem für Teilaufgabe b)) ist die Frage, wie die einzelnen Geschwindigkeits-Boosts miteinander stacken. Wir haben die Aufgaben absichtlich so gebaut, dass die Kombination in Teilaufgabe a) leicht ist - während bei Aufgabe b) genau darauf zu achten ist, ob die Boosts sich beispielsweise gegenseitig erhöhen oder nicht. Wir gehen darauf noch einmal im Detail in der Lösung zu Teilaufgabe b) ein.
Den Ausgangswert bildet die Geschwindigkeit von 8, welche aufgrund des Einheitenspeeds von 3 verdreifacht wird:
8 * 3 = 24
Im nächsten Schritt rechnen wir den Leuchtturm auf die Geschwindigkeit an:
24 * 1,15 = 27,6
Und im nächsten Schritt die Verbesserte Truppenbewegung:
27,6 * 1,3 = 35,88
Da es sich hierbei nicht um Sekunden handelt, durfte nicht gerundet werden. Die Geschwindigkeit unseres Transportboots unter den Bedingungen in Teilaufgabe a) ist nun also 35,88.
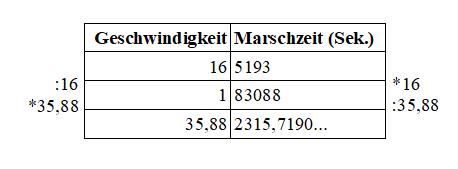
Ich nutze (weil ich es als anschaulich und übersichtlich empfinde) jetzt den Dreisatz, um die entsprechende Marschzeit zu bestimmen, die bei einer Geschwindigkeit von 35,88 besteht:
Die Aussagen des Dreisatzes sind:
- Wenn die Geschwindigkeit 16 beträgt, ist die Marschzeit 5193 Sekunden.
- Wenn die Geschwindigkeit 1 beträgt, ist die Marschzeit 83088 Sekunden.
- Wenn die Geschwindigkeit 35,88 beträgt, ist die Marschzeit 2315,7190 Sekunden.
In unserer Aufgabe war jedoch angegeben, dass alle Sekunden-Werte auf ganze Zahlen abgerundet werden müssen, bevor weitergerechnet wird. Insofern ergibt sich eine Marschzeit von 2315 Sekunden, wenn die in Teilaufgabe a) beschriebene Situation besteht.
Um jetzt die Laufzeit zu ermitteln, nach der gefragt war, müssen Rüst- und Marschzeit addiert werden:
300 Sekunden + 2315 Sekunden = 2615 Sekunden
Dieses Ergebnis muss nun noch in das Format Stunden : Minuten : Sekunden gebracht werden (das lässt sich ggf. auch eleganter lösen):
2615 Sekunden / 60 Sekunden = 43,... Minuten
43 Minuten * 60 Sekunden = 2580 Sekunden
2615 Sekunden - 2580 Sekunden = 35 Sekunden
Das Endergebnis für Teilaufgabe a) lautet dann also:
00:43:35 Stunden.
Zu b)
Um für dieselbe Strecke wie in Aufgabe a) für ein Kolonieschiff die richtige Laufzeit (unter Berücksichtigung aller anderen Angaben) zu finden, müssen wir ebenfalls mit den entsprechenden Geschwindigkeiten arbeiten. Wir fragen uns also: Was für eine Geschwindigkeit hat das Kolonieschiff unter den Bedingungen in Teilaufgabe b)?
Zu berücksichtigen sind nun:
- Kolonieschiff: Geschwindigkeit 3 (s. Wiki)
- Einheitenspeed 3
- Bonus "Verbesserte Truppenbewegung": Einheiten bewegen sich 30% schneller
- Spezialgebäude "Leuchtturm": Einheiten bewegen sich 15% schneller
- Forschung "Segel setzen": Kolonieschiffe bewegen sich 10% schneller
- Atalanta mit Stufe 13: Einheiten bewegen sich 23% schneller (auf Stufe 1: 11%, je weiterer Stufe kommt dann 1% hinzu)
Was nun die (unserer Meinung nach) krasse Schwierigkeit der Aufgabe ausmacht, war es, durch eigene Tests herauszufinden, dass sich diese Geschwindigkeits-Boosts nicht mehr so einfach stacken lassen wie in Teilaufgabe a). Es kommt nun genau darauf an, wie man rechnet und welche Zahlen man worauf bezieht.
Wir würden die oben genannten Faktoren dabei in drei Kategorien einteilen: in die stabilen Grundwerte, in die permanenten und die temporären Geschwindigkeits-Boosts.
- Stabile Grundwerte sind die Geschwindigkeiten der einzelnen Einheiten und der Einheitenspeed einer Spielwelt. Diese sind für alle Befehle gleich und können von den Spielerinnen und Spielern nicht beeinflusst werden.
- Permanente Geschwindigkeits-Boosts sind der Leuchtturm und Segel setzen (und beispielsweise auch noch Kartographie oder Meteorologie). Diese Faktoren zeichnen sich durch Kontinuität aus, müssen aber erst durch die Spielerin oder den Spieler aktiviert werden.
- Als temporäre Geschwindigkeits-Boosts würden wir die Verbesserte Truppenbewegung und Atalanta bezeichnen. Der Bonus verfällt nach seiner Laufzeit, der Held muss bei jedem Angriff ausgewählt werden, kann einer anderen Stadt zugewiesen oder verwundet werden.
Je nach Kategorie unterscheidet sich auch, wie sich die Faktoren auf die Geschwindigkeit auswirken.
Die stabilen Grundwerte bilden insofern eine Einheit: Sie sind die Basis für alle weiteren Berechnungen. Sie werden miteinander multipliziert. Im konkreten Fall also:
3 * 3 = 9
Die permanenten Geschwindigkeits-Boosts beziehen sich auf die stabilen Grundwerte - allerdings nicht aufeinander. Ihre Effekte werden also hinsichtlich der Grundwerte jeweils isoliert berechnet und dann auf die Grundwerte addiert. Im konkreten Fall (Klammern zur Veranschaulichung):
9 + (9 * 0,15) + (9 * 0,1) = 9 + 1,35 + 0,9 = 11,25
Die temporären Geschwindigkeits-Boosts wiederum beziehen sich nun auf die Geschwindigkeit inklusive der permanenten Geschwindigkeits-Boosts. Auch die temporären Boosts beziehen sich jedoch nicht aufeinander, sondern werden isoliert berechnet und dann aufaddiert:
11,25 + (11,25 * 0,3) + (11,25 * 0,23) = 11,25 + 3,375 + 2,5875 = 17,2125
Falsch wäre es beispielsweise gewesen zu rechnen:
3 * 3 * 1,15 * 1,1 * 1,3 * 1,23 = 18,204615
In Teilaufgabe a) war es jedoch noch möglich, auf diese Weise zu rechnen, weil es nur jeweils einen Geschwindigkeits-Boost aus den beiden Kategorien gab.
Die Geschwindigkeit unseres Kolonieschiffes ist insofern also 17,2125. Dank der Vorarbeit in Teilaufgabe a) wissen wir:
"Wenn die Geschwindigkeit 1 beträgt, ist die Marschzeit 83088 Sekunden."
Bei einer Geschwindigkeit von 17,2125 beträgt die Marschzeit dann also: 83088 / 17,2125 = 4827,1895... Sekunden. Abgerundet sind das 4827 Sekunden.
Da wir uns weiterhin auf einer Welt mit einem Weltspeed von 3 befinden, beträgt die Rüstzeit 300 Sekunden, die Laufzeit des Kolonieschiffes also 5127 Sekunden.
Diese sind nun noch ins richtige Format zu bringen:
5127 Sekunden / 60 Sekunden = 85,... Minuten
85 Minuten * 60 Sekunden = 5100 Sekunden
5127 Sekunden - 5100 Sekunden = 27 Sekunden
85 Minuten = 1 Stunde, 25 Minuten
Das Ergebnis für Teilaufgabe b) ist damit:
01:25:27 Stunden.
Hinweise: Die hier angestellten Rechnungen sind umständlicher als es nötig gewesen wäre. Die Erklärungen hier sollen vor allem anschaulich sein. Es gab auch Lösungen, die im Ergebnis leicht von den hier eingestellten abweichen, ohne dass sie falsch wären. Das liegt an zulässigen Zwischenschritten, bei denen korrekterweise abgerundet wurde.
Von 7 Teilnehmern hat einer diese Aufgabe korrekt beantwortet: @IDontMainLulu - der unser Grepolis Schlaumeier 2021 ist! Einen ganz herzlichen Glückwunsch zu diesem herausragenden Erfolg, insbesondere als Fremdsprachler!

Die Plätze 2 und 3 sind allerdings noch zu vergeben, weshalb die verbliebenen 6 Teilnehmer folgende Aufgabe in der
24. Runde lösen müssen:
Spieler A greift Spieler B mit 5 Hydren, 3 Feuerschiffen und 4 Triremen an. Spieler B wirkt "Seesturm" auf den Angriff, wobei die Stärke des Effekts 25% beträgt. Nenne alle möglichen Kombinationen an zerstörten Einheiten.